To help those who are curious about what Singapore Math is all about, this series of blog posts will take you through the history, approach, and essentially the “why” of Singapore Math. These conversations will largely draw from a paper written by SLO Classical Academy graduate, Sadie Richert.
Our first post in this series explored the background of the Singapore Math Curriculum, including how and why it came to the United States. Today, Sadie explores a couple of the core tenants of this curriculum: the “Concrete-Pictorial-Abstract” (CPA) method and bar modeling. Let’s dive in:
Central to the Singapore Primary Mathematics curriculum is the model method—which is a problem-solving strategy that fosters algebraic thinking in young students. If students can visualize the problem in their heads well, they will easily be able to solve more and more complex problems. To visualize well in their minds, they need to first move numbers with their fingers so they can move numbers in their minds.
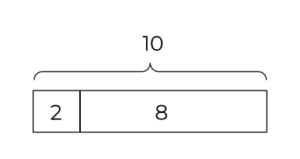
In a publication by the National Council of Teachers of Mathematics, Lisa Englard notes that young children naturally “construct strategies for problem-solving that model the actions and relationships present in a problem.” Also known as “bar modeling”, the model method promotes this inclination by teaching students to “visually represent and explore the relationships within a problem situation” using rectangular bars. For the youngest students first exploring the properties of numbers, a part-whole model can visually represent number bonds—the concept that a number can be split into two smaller numbers, as illustrated below.
Bar models also become an invaluable tool in solving word problems. Rather than falling prey to sloppy shortcuts such as guessing which operation to use based on keywords or numbers found in a question, students are able to conceptualize the actual relationships between elements of a word problem when they use a visual representation such as a comparison model. While other curriculums highlight keywords that signal to students which operations should be used in a given scenario (such as “times” indicating multiplication), this approach is misleading. For example, a case study testing 4-6th graders who had been taught math with and without the model method offered this problem:
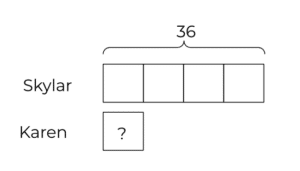
Skylar has 4 times as many books as Karen.
If Skylar has 36 books, how many books does Karen have?
A student who assumes the word “times” indicates multiplication will solve this problem incorrectly. Instead, a student using the model method to represent the situation will recognize that one must divide 36 by 4 to see how many books Karen has. The drawing below demonstrates a way this material might be represented:
As Swee Fong Ng and Kerry Lee noted in a study published by the Journal for Research in Mathematics Education, students who attempt problems using the model method gain the excellent opportunity to “reflect on the representation, make modifications, and select a solution strategy.” According to Ng and Lee, these tactics benefit adults and children alike since “representing a given word problem and…identifying the appropriate computation” is more of a factor in determining success in problem solving than rote algorithmic skill. Notably, visual representations provide students with a pictorial stepping stone towards higher-order reasoning without requiring a conception of “formal symbolic algebra.” Students are “essentially writ[ing] equation[s] to model situation[s] but us[ing] bar[s] instead of variable[s].” Teaching students to visually represent information and then seek appropriate strategies to analyze it, the model method unites structural and procedural thought-processes with a versatility for use across grade levels.
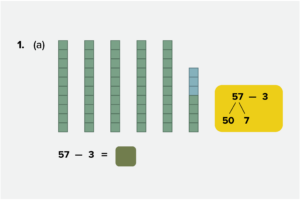
Example of how the bar model would be used to conceptualize a subtraction problem for younger students.
The model method is a facet of the Concrete-Pictorial-Abstract approach to math education, inspired by children’s natural inclinations to conceptualize numbers. Mathematical expressions are introduced to the youngest students via tangible representations, building “an understanding of abstract mathematical concepts from everyday experiences and meaningful contexts.”
While critics of Primary Mathematics often complain that this approach requires a hefty investment in special manipulatives for use in lessons, there is no special formula of what to use. Colored milk-carton caps work splendidly as counters to represent addition and subtraction problems; home-made paper circles make excellent fraction pies (as does actual pie!). Regardless of their type, concrete representations of concepts are invaluable in helping students internalize numerical principles. Students encountering problems of increasing complexity (or simply larger numbers) will later transition to the pictorial stage of bar modeling and eventually are equipped for the final “abstract” stage of mathematical reasoning.

Next up in the “Why Singapore Math” series, we will discuss Singapore Math’s unique Spiral-Mastery approach, as well as a crucial element of this curriculum: mental math!
There are now several Singapore-based math curricula available in the United States. WWP recommends Primary Mathematics for K-5th and Dimensions for grade 6. To see full samples of our video teaching series for Singapore math home instructors or school instructors, click here.
Sadie Richert wrapped up her senior year in high school with Calculus 3 (completed at CSU Cal Poly). She is currently pursuing a Bachelor of Music degree in violin, with elective studies in Mathematics and a Classical Languages minor at Wheaton College.







